Nilai Mutlak

Penjelasan Tentang Nilai Mutlak

Nilai mutlak merupakan salah satu materi dalam kelas X dimana, konsep nilai mutlak ini harus bener-bener temen-temen pahami agar temen-temen tidak merasa kesulitan ketika mengerjakan soal nilai mutlak. Oleh karena itu, Rumus Matematika kali ini akan mengulas mengenai konsep Nilai mutlak untuk membantu temen-temen dalam memahami materi nilai mutlak ini.

Penjelelasan Tentang Nilai Mutlak

Misalnya x merupakan variabel pengganti bilangan real, dimana karena x anggota himpunan bilangan real maka dapat ditulis x∈R. Secara geometris, nilai mutlak suatu bilangan yaitu jarak antara bilangan itu dengan nol pada garis bilangan real. Oleh sebab itu, tidak mungkin nilai mutlak suatu bilangan bernilai negatif, tetapi mungkin saja bernilai nol. Sehingga nilai mutlak x, kita definisikan sebagai berikut. Berdasarkan definisi diatas, berarti bahwa nilai mutlak bilangan positif atau nol adalah bilangan itu sendiri dan nilai mutlak dari suatu bilangan negatif adalah lawan dari bilangan negatif itu. contoh : |2| = 2 |-5| = 5 |¾| = ¾

Persamaan Nilai Mutlak

Perhatikan sifat nilai mutlak berikut. Untuk setiap a, b, c dan x bilangan real dengan a≠0.

1. Jika |ax+b| = c dengan c≥0, maka salah satu sifat berikut ini berlaku yaitu |ax+b|=c untuk x≥-b/a  dan  -(ax+b)=c untuk x<-b/a.
2. Jika |ax+b| = c dengan c<0, maka tidak ada bilangan real x yang memenuhi persamaan  |ax+b| = c.

cara menyelesaikan persamaan nilai mutlak. misalnya terdapat persamaan |x-p|=q maka akibatnya, |x-p|=q berubah menjadi

Menyelesaikan Persamaan Nilai Mutlak

Posted on 17 November 2013 by Yosep Dwi Kristanto

Nilai mutlak dari suatu bilangan x dapat diartikan sebagai jarak bilangan tersebut terhadap titik 0 pada garis bilangan, dengan tidak memperhatikan arahnya. Ini berarti |x| = 5 memiliki dua selesaian, karena terdapat dua bilangan yang jaraknya terhadap 0 adalah 5: x = –5 dan x = 5 (perhatikan gambar berikut).

Konsep ini dapat diperluas untuk situasi yang melibatkan bentuk-bentuk aljabar yang berada di dalam simbol nilai mutlak, seperti yang dijelaskan oleh sifat berikut.

Sifat Persamaan Nilai Mutlak
Jika X merupakan suatu bentuk aljabar dan k adalah bilangan real positif, maka |X| = k akan mengimplikasikan X = –k atau X = k.

Seperti yang dinyatakan dalam sifat persamaan nilai mutlak, sifat ini hanya dapat diterapkan setelah kita mengisolasi simbol nilai mutlak pada satu ruas. Untuk lebih jelasnya perhatikan contoh berikut.
Contoh 1: Menyelesaikan Persamaan Nilai Mutlak
Selesaikan persamaan: –5|x – 7| + 2 = –13.
Pembahasan Pertama, kita isolasi nilai mutlak, yaitu membuat simbol nilai mutlak berada pada satu ruas sedangkan suku-suku lainnya kita letakkan di ruas yang lain.

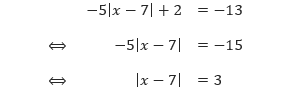
Sekarang perhatikan bahwa x – 7 merupakan “X” pada sifat persamaan nilai mutlak, sehingga

Dengan mensubstitusi ke persamaan semula akan memastikan bahwa himpunan selesaiannya adalah {4, 10}.
Catatan Untuk persamaan seperti pada contoh 1 di atas, hati-hati untuk tidak memperlakukan simbol nilai mutlak seperti tanda kurung biasa. Persamaan –5(x – 7) + 2 = –13 hanya memiliki selesaian x = 10, dan tidak memiliki selesaian kedua karena persamaan tersebut memiliki bentuk sederhana x – 7 = 3. Persamaan –5|x – 7| + 2 = –13 dapat disederhanakan menjadi |x – 7| = 3 yang memiliki dua selesaian.
Persamaan nilai mutlak dapat muncul dari berbagai bentuk. Tetapi dalam menyelesaikan persamaan tersebut, kita harus mengisolasi simbol nilai mutlak baru kemudian menerapkan sifat persamaan nilai mutlak.
Contoh 2: Menyelesaikan Persamaan Nilai Mutlak
Tentukan himpunan selesaian dari persamaan: |5 – 2/3 x| – 9 = 8.
Pembahasan Dengan mengisolasi simbol nilai mutlak baru kemudian menerapkan sifat persamaan nilai mutlak, kita mendapatkan

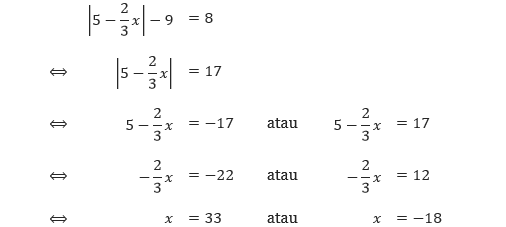
Sehingga, himpunan selesaian dari persamaan tersebut adalah {–18, 33}.
Untuk beberapa persamaan, seringkali kita membutuhkan sifat perkalian persamaan nilai mutlak untuk menyelesaikannya.

Sifat Perkalian Persamaan Nilai Mutlak
Jika A dan B adalah bentuk-bentuk aljabar, maka |AB| = |A||B|.

Perhatikan bahwa jika A = –1 maka menurut sifat tersebut |–B| = |–1||B| = |B|. Secara umum, sifat tersebut berlaku untuk sembarang konstanta A.
Contoh 3: Menggunakan Sifat Perkalian Persamaan Nilai Mutlak
Tentukan selesaian dari persamaan: |–2x| + 5 = 13.
Pembahasan Seperti pada contoh-contoh sebelumnya, kita harus mengisolasi simbol nilai mutlak baru dapat mengaplikasikan sifat-sifat persamaan nilai mutlak.

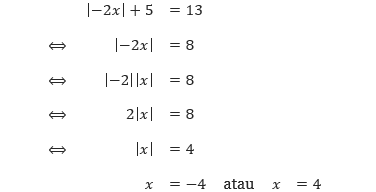
Diperoleh selesaian dari persamaan tersebut adalah x = –4 atau x = 4. Semoga bermanfaat, yos3prens.

Penjelasan Tentang Bilangan Real, Garis Bilangan.

Pengertian dan contoh Bilangan Real, Rasional, Irrasional, Bulat, Cacah, Asli, dan Bilangan Prima

Ada beberapa istilah bilangan pada Matematika, yakni Bilangan Real, Rasional, Irrasional, Bulat, Asli, Prima, dan Bilangan Cacah, pengertian ini merupakan sebuah dasar dalam ilmu matematika. Bila sobat tidak hafal maupun tahu tentang beberapa bilangan matematika, maka nantinya akan sulit. Dalam tingakatan SD, SMP, dan SMA bilangan ini sering dibahas, maka dari itu berikut masing-masing pengertiannya.

1. Bilangan Real
   Bilangan real adalah bilangan yang merupakan gabungan dari bilangan rasioanal dan bilangan irrasioanal sendiri.
   Contohnya :
   0, 1, 2, ½, 4/7, 55/7, √2, √3, √5, .... dan seterusnya.
   
   
2. Bilangan Rasional
   Bilangan Rasional yaitu bilangan dalam bentuk a/b, dengan a dan b anggota bilangan bulat dan b  ≠ 0.
   Contohnya :
   1/4 menjadi a = 1 dan b = 4
   
   
3. Bilangan Irrasional
   Bilangan irrasional adalah bilangan-bilangan yang tidak dapat dinyatakan sebagai pecahan, atau bilangan yang bukan bilangan rasional.
   Contohnya :
   √2, √3, √5
   
   NB :
   √9 = 3, maka √9 bukan bilangan irrasional.
   
   
4. Bilangan Bulat
   Bilangan bulat yaitu bilangan yang terdiri atas bilangan negatif, bilangan 0 (nol), dan bilangan postitif, yaitu : ..., -2, -1, 0, 1, 2, 3, ... , dan seterusnya.
5. Bilangan Cacah
   Bilangan cacah yaitu bilangan yang dimulai dari angka 0 (nol) sampai tak terhingga, yaitu: 0, 1, 2, 3, 4, 5, 6, ..., dan seterusnya.
6. Bilangan Asli
   Bilangan Asli yaitu bilangan yang dimulai dari angka 1 (satu) sampai tak terhingga, yaitu: 1, 2, 3, 4, 5, 6, ..., dan seterusnya.
7. Bilangan Prima
   Bilangan Prima yaitu bilangan asli yang tepat mempunyai 2 faktor, yaitu 1 dan bilangan itu sendiri, yaitu: 2, 3, 5, 7, 11, 13,  ..., dan seterusnya.
8. Garis bilangan (bahasa Inggris: number line) dalam matematika dasar adalah suatu gambar garis lurus di mana setiap titiknya diasumsikan melambangkan suatu bilangan real dan setiap bilangan real merujuk pada satu titik tertentu.^[1] Seringkali bilangan bulat ditunjukkan dengan lambang titik-titik tertentu yang berjarak sama di sepanjang garis ini.
   Misalnya, gambar di bawah ini menunjukkan bilangan bulat dari −9 sampai 9. Meskipun demikian, garis ini mencakup semua bilangan real, berkelanjutan tak terhingga ke kedua arahnya, dan juga bilangan-bilang tak bertanda yang terdapat di antara bilangan-bilangan bulat itu. Biasanya digunakan sebagai alat bantu dalam mengajar penjumlahan dan pengurangan sederhana, khususnya yang melibatkan bilangan negatif.
   
   
   Garis di atas dibagi menjadi dua belahan simetri oleh titik nol (origin), yaitu yang melambangkan bilangan nol.
   Dalam matetmatika lanjutan, ekspresi "garis bilangan real" (real number line atau real line) biasanya dipakai untuk melambangkan konsep di atas, yaitu setiap titik pada garis lurus ini melambangkan satu bilangan real tertentu, dan vice versa ("sebaliknya").
   

   Menggambar garis bilangan

   Garis bilangan biasanya digambar sebagai suatu garis horisontal. Bilangan positif selalu terletak di kanan titik nol, dan bilangan negatif selalu di sebelah kiri titik nol. Sebuah ujung panah ditempatkan di kedua ujung untuk menandakan bahwa garis ini akan berlanjut dengan bilangan real (dilambangkan dengan ${\displaystyle \mathbb {R} }$) positif dan negatif sampai tak terhingga. Bilangan real terdiri dari bilangan irasional maupun bilangan rasional, yang meliputi pula bilangan bulat, bilangan cacah, dan bilangan asli.
   Sebuah garis yang digambar melalui titik nol dengan arah tegak lurus dari garis bilangan real dapat pula digunakan untuk melambangkan bilangan imaginer. Garis tegak lurus ini, disebut garis imaginer, memperluas garis bilangan menjadi suatu bidang bilangan kompleks, yang titik-titiknya melambangkan bilangan-bilangan kompleks
    

Macam Macam Bilangan dan Pengertiannya.

Pengertian Bilangan

Bilangan adalah suatu konsep matematika yang digunakan sebagai pencacahan dan pengukuran. Lambang atau simbol untuk mewakili bilangan disebut dengan angka atau lambang bilangan.

Macam-Macam Bilangan

Terdapat berbagai macam jenis bilangan, berikut ini adalah penjelasan tentang macam-macam bilangan beserta contohnya lengkap.

Bilangan Asli

Pengertian bilangan asli adalah bilangan positif yang di mulai dari bilangan satu keatas. Contohnya: N = {1, 2, 3, 4, 5, 6, 7….}

Bilangan Bulat

Pengertian bilangan bulat adalah himpunan bilangan bulat negatif, bilangna nol dan bilangan bulat positif. Contohnya: B = {…., -4, -3, -2, -1, 0, 1, 2, 3, 4,…..} 

Bilangan Cacah

Pengertian bilangan cacah adalah himpunan bilangan yang terdiri bilangan positif danb nol. Contohnya : C = {0, 1, 2, 3, 4, 5, 6, 7, 8,….}

Bilangan Prima

Pengertian bilangan prima adalah bilangan yang tidak dapat dibagi oleh bilangan lainnya kecuali bilangan itu sendiri dan 1. Contohnya: P = {2, 3, 5, 7, 11, 13, 17, …..}Bilangan Nol

Pengertian bilangan nol adalan bilangan nol (0) itu sendiri. Contohnya: N = {0}

Bilangan Pecahan

Pengertian bilangan pecahan adalah bilangan yang dapat dinyatakan dalam bentuk a/b dengan a dan b adalah bilangan bulat dan b ≠ 0. Bilangan a disebut dengan pembilang dan b disebut dengan penyebut. Contohnya: H = { ⅓, ⅔, ⅛, ⅝, ….. }
Keterangan: 4/2 = 2, berarti 4/2 bukan bilangan pecahan.

Bilangan Rasional

Pengertian bilangan rasional adalah bilangan yang dinyatakan dalam bentuk a/b dengan a dan b merupakan anggota bilangan bulat dan b ≠ 0. Contohnya: R = { ¼, ¾, …. }

Bilangan Irrasional

Pengertian bilangan irrasional adalah himpunan bilangan yang tidak dapat dinyatakan dalam bentuk pecahan atau bilangan sekain bilangan rasional. Contohnya : I = { √2, √3, √5, √6, √7, ….. }
Keterangan √9 = 3 berarti √9 bukan bilangan irrasional.

Bilangan Real

Pengertian bilangan real adalah himpunan bilangan berupa gabungan antara bilangan rasional dan bilangan irasional. Contohnya: R = { 0, 1, ¼, ⅔, √2, √5, ….. }

Bilangan Negatif

Pengertian bilangan negatif adalah bilangan yang bernilai negatif. Contohnya: N = { -3, -5, ¼, …. }
Keterangan -1/-4 = ¼, jadi -1/-4 bukan bilangan negatif.

Bilangan Positif

Pengertian bilangan positif adalah bilangan yang bernilai positif selain nol. Contohnya: P = {2, 3, 4, 5, ¼, ….}

Bilangan Genap

Pengertian bilangan genap adalah bilangan-bilangan yang akan habis jika dibagi menjadi 2. Contohnya: Ge = {2, 4, 6, 8, 10, 12, ….}

Bilangan Ganjil

Pengertian bilangan ganjil adalah bilangan yang jika dibagi 2 maka akan tersisa 1 atau bilangan yang dapat dinyatakan dengan 2n-1 dengan n adalah bilangan bulat. Contohnya: Ga = {-3, -1, 1, 3, 5, 7, 9, 11, …. }

Bilangan Komposit

Pengertian bilangan komposit adalah bilangan asli yang lebih besar dari 1 tapi bukan termasuk dalam bilangan prima. Contohnya: K = {4, 6, 8, 9, 10, 12, ….}

Bilangan Riil

Pengertian Bilangan Riil adalah bilangan yang dapay ditulis dalam bentuk desimal. Contohnya: L = { 5/8, log 10, ….}

Bilangan Imajiner

Pengertian bilangan imajiner adalah bilangan i (satuan imajiner), dimana i merupakan lambang bilangan baru yang bersifat i2 = -1. Contohnya: I = {i, 4i, 5i, …..}

Bilangan Kompleks

Pengertian bilangan kompleks adalah bilangan yang anggotanya a+bi, dimana a,b ϵ R, i2 = -1. Dengan a bagian bilangan riil dan b bagian bilangan imajiner. Contohnya K = {2-3i, 8+2, …..}

Bilangan Kuadrat

Pengertian bilangan kuadrat adalah bilangan yang dihasilkan dari perkalian suatu bilangan dengan bilangan itu sendiri sebanyanyak dua kali dan disimbolkan dengan pangkat 2.
Contohnya : K = {2², 3²,4²,5²,6²,….}

Bilangan Romawi

Pengertian bilangan romawi adalah suatu sistem penomoran yang berasal dari romawi kuno menggunakan huruf latin yang melambangkan angka numerik. Contoh: M = {I, II, III, IV, V, VI, VII, VIII, XI, X, XI,…..}