Invers matriks menggunakan metode adjoin, Perkalian Elementer dan patrisi

Invers Matriks menggunakan metode adjoin dengan n=4




Cara paling mudah adalah dengan metode Sarrus
Determinan berdasarkan gambar di atas:

Sedangkan Matriks Inversnya:

Dengan b₁₁ hingga b₄₄ diperoleh dari perhitungan:

Matriks Elementer

Matriks elementer adalah matriks identitas yang dikenai satu kali OBE.
Contoh :

Jika E suatu matriks elementer berordo m´m, dan A suatu matriks berordo m´n maka EA hasilnya akan sama dengan matriks yang diperoleh dari A dengan melakukan operasi baris elementer yang sesuai.

Contoh :


                          
                          

Invers Matriks Menggunakan Metode Partisi

Operasi matriks memang sudah sama-sama kita pelajari di bangku SMA. Banyak sekali manfaat dari adanya matriks, salah satunya adalah untuk memudah penyelsaian persamaan simultan. Tipe matriks, Operasi penjumlahan, perkalian, transpose, determinan, kofaktor, adjoin dan proses invers matriks dibahas detail dengan contoh-contoh soal yang representatif. 

Berikut adalah beberapa materi penting terkait perhitungan matriks dengan sumber “Modern Power System Control” oleh Prof. Dr. Ir. Imam Robandi, MT.

MENGINVERSE MATRIKS MENGGUNAKAN METODE PARTISI

Matriks sangat penting dalam penyelesaian Multi-Equation Multi-Variable (MEMV), berikut adalah contoh MEMV

Persamaan diatas dapat dinyatakan dalam bentuk matriks dengan komponenya yaitu matriks koefisien, matriks variabel dan matriks output sebagai berikut

Dari persamaan tersebut maka persamaan awal dapat dinyatakan dengan

Dengan hanya berbekal kemampuan menguasai invers matrix dengan dimensi 2x2, maka kita dapat melakukan invers matriks yang berdimensi mxn dengan sangat mudah. Motode partisi dapat membantu perhitungan invers dari matriks-matriks yang berorder tinggi. Matriks inversi A dinotasikan dengan A^-1 yang merupakan pembagian adjoin matriks A dengan determinannya, seperti berikut

Dari persamaan tersebut, maka diketahui bahwa dimensi matriks A sangat besar, maka perhitungan adjoin dan determinannya menjadi sangat rumit. Oleh karena itu, perlu pemecahan menggunakan metode partisi agar dimensi matriks menjadi lebih kecil.

Metode partisi adalah salah satu metode yang dapat digunakan untuk menginverse matriks yang berdimensi besar. Sebuah matriks yang akan dicari inversnya dipartisi menjadi 4 matriks sebagai berikut:

 

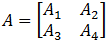
Syarat utama dari proses partisi adalah matriks A₁  dan A₄ harus bujur sangkar. Untuk memudahkan pengoperasian inversi dari matriks A yaitu A^-1 dapat ditulis sebagai berikut: